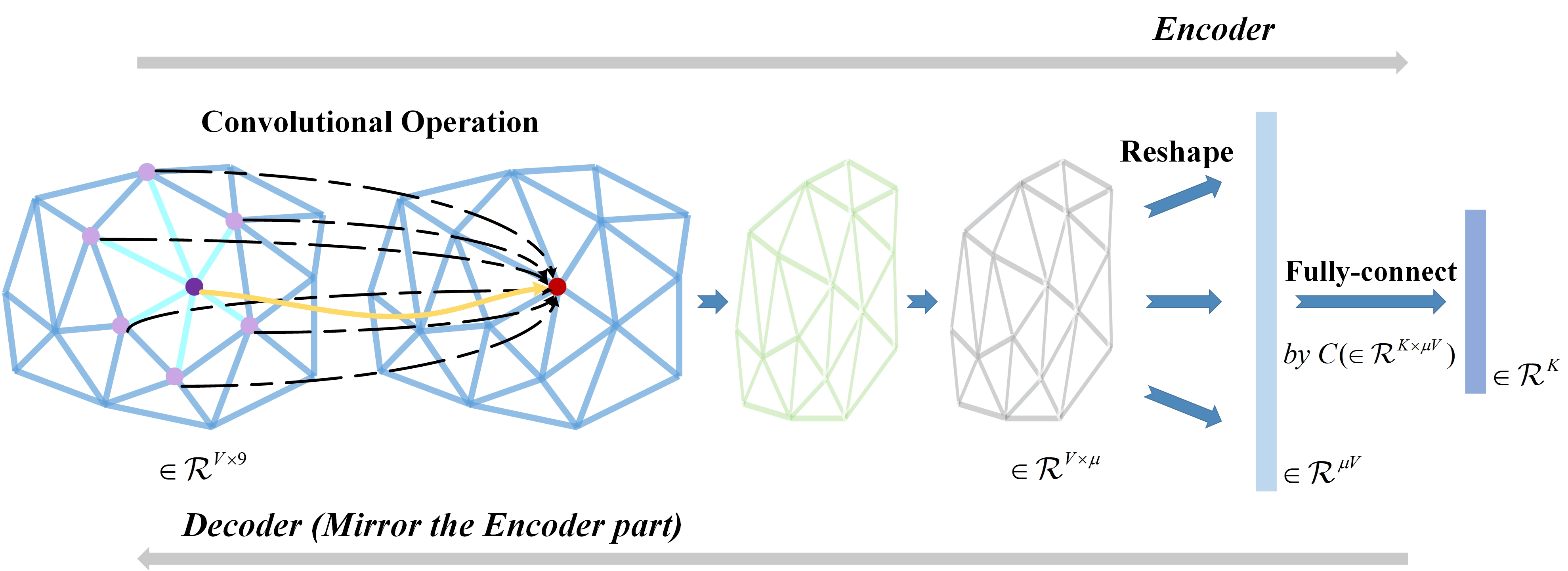
 The proposed network architecture.
The proposed network architecture.
Abstract
Spatially localized deformation components are very useful for shape analysis and synthesis in 3D geometry processing. Several methods have recently been developed, with an aim to extract intuitive and interpretable deformation components. However, these techniques suffer from fundamental limitations especially for meshes with noise or large-scale deformations, and may not always be able to identify important deformation components. In this paper we propose a novel mesh-based autoencoder architecture that is able to cope with meshes with irregular topology. We introduce sparse regularization in this framework, which along with convolutional operations, helps localize deformations. Our framework is capable of extracting localized deformation components from mesh data sets with large-scale deformations and is robust to noise. It also provides a nonlinear approach to reconstruction of meshes using the extracted basis, which is more effective than the current linear combination approach. Extensive experiments show that our method outperforms state-of-the-art methods in both qualitative and quantitative evaluations.